【导读】谐波是数字电路产生的一种噪声源。如果能够很好地控制谐波,便能有效抑制数字电路产生的噪声。本章节将讲述数字信号所包括谐波的基本性质。
谐波的本质(就噪声而言)
(1) 数字信号是由谐波组成的
通常而言,具有恒定循环周期的所有波形都可以分解为包括循环频率和谐波的基波,其中谐波的频率为循环频率的整数倍。基波的倍数称为谐波次数。
在精确重复波的情况下,除此之外没有任何其它频率成分。数字信号有很多循环波形。因此,在测量频率分布(称为“频谱”)时,可以精确分解为谐波,显示出离散分布的频谱。
(2) 测量时钟脉冲信号的谐波
图1显示了频谱分析仪测量的33MHz时钟脉冲信号谐波的示例。像针一样向上突起的部分为谐波,其出现的间隔正好为33MHz。可以发现奇次谐波和偶次谐波的趋势不一样。最下面部分约为40dB或更低,指示频谱分析仪的背景噪声。
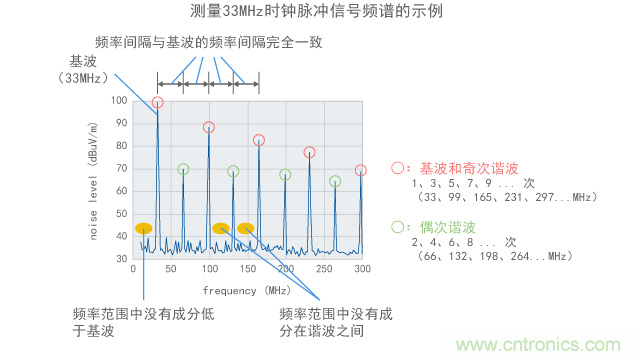
图1 谐波的本质
(3) 如何从噪声频率中找出噪声源
上面提及的谐波性质有助于根据噪声频率找出噪声源。通过测量噪声频谱间隔,可以类比推导出造成噪声的信号循环频率。例如,我们在电子设备中观察到了 如图2所示的噪声。出现强烈噪声的频率的间隔似乎是33MHz。因此,可以认为噪声是与33MHz时钟同步运行的电路造成的。
即使此电子设备当前使用的电路具有非常接近的循环频率,如33.3MHz或34MHz,如果可以精确测量噪声频率和间隔,就可分离出这样的频率。例如,如 果在图2中330MHz处存在噪声,则可以假设噪声是由33.0MHz的电路而不是33.3MHz的电路所造成的。这是因为33.3MHz或 34MHz信号都不包括330MHz谐波。
(4) 只包括整数倍频率
此外,循环波形并不包括低于基频的任何频率成分。例如,100MHz信号绝不会产生20MHz、50MHz或90MHz的噪声。如果出现此种频率,则噪声是由分频信号而不是源信号所导致的。数字电路通常与时钟脉冲信号同步运行,而且很多数字电路的运行频率为时钟脉冲信号的1/N(称为“分频”)。在这种情况下,谐波是分频信号频率的整数倍。 但是,如果两个或更多电路以经过分频的相同时钟脉冲信号运行,时钟脉冲信号的谐波会与分频信号的谐波相互重叠,导致难以对其进行区分。
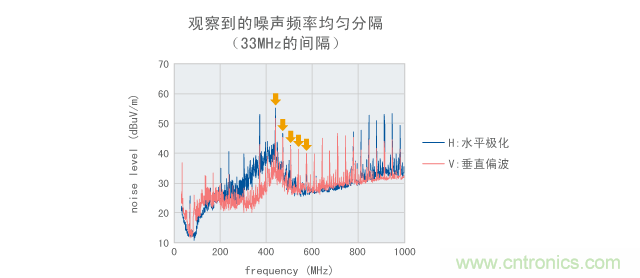
图2 明确显示谐波的噪声测量结果的示例
[page]谐波的复合波形
(1) 与正弦波叠加接近数字波形
数字信号波形及其包括的谐波是如何相互关联的?图3显示了将低次谐波与基波相加时波形的变化。可以发现,随着加上各个谐波,原基波的正弦波形越来越接近矩形波。
(2) 高次谐波对波形的影响小
相反,当从理想的矩形波减去高次谐波时,波形越来越接近正弦波。但是,变化很小。例如,图4显示了从叠加到第17次谐波上的波形中依次减去最高谐波后的波形。
(3) 占空50%的波形具有很强的奇次谐波
当形成占空比为50%的波形时,仅叠加奇次谐波。如果形成的波形不具有50%的占空比,也需要章节5所述的偶次谐波。此处的占空比指的是一个循环中信号电平“高”的比例。在现实世界的波形中,占空比不可能正好为50%。所以,偶次谐波也包括在内了,如图1所示。
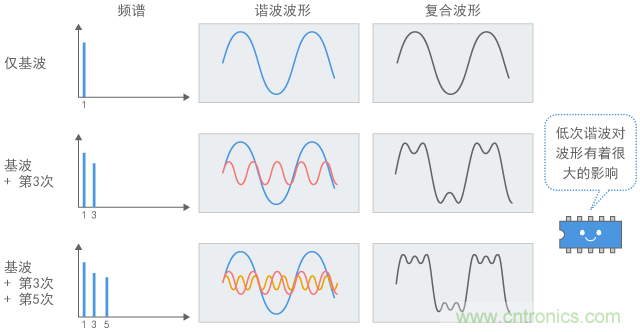
图3 谐波和信号波形(1): 加上低次谐波
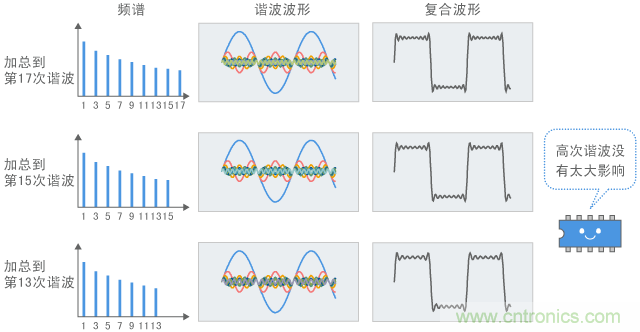
图4 谐波和信号波形(2): 减去高次谐波
(4) 通过减去高次谐波降低噪声
前已述及,数字信号谐波中相对较低的频率(低次)成分对保持信号波形很重要,而较高的频率(高次)成分则不太重要。
但是,如章节2-3-6“信号中的谐波”所述,高次谐波具有更高的频率,因而具有容易发射和造成噪声的性质。因此,通过在不对信号波形造成任何问题的范围 内消除高次谐波来抑制噪声。通常最多保留第3倍到第7倍的谐波,并消除比这大的所有谐波。图5显示了使用低通滤波器消除谐波时波形和噪声的测量结 果。去除谐波之后,数字信号的波形具有这样的圆角而不是合适的方角。
(5) 通过信号EMI静噪滤波器消除谐波
信号EMI静噪滤波器正是用于此目的的滤波器。在图5中,20MHz信号使用了截止频率为150MHz的EMI静噪滤波器。因此,图(b)中的波形最多包括7次谐波(140MHz)。EMI静噪滤波器将在后续章节中进一步讲述。
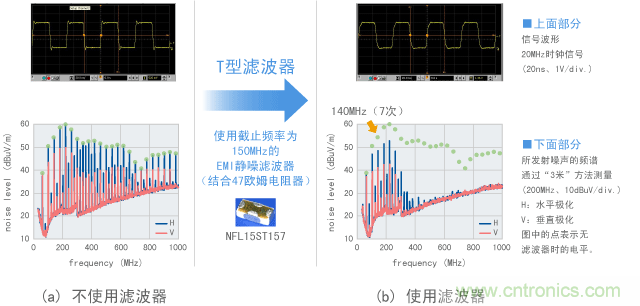
图5 已通过EMI静噪滤波器消除谐波的信号波形和噪声的示例
[page]谐波频率的趋势
(1) 梯形波谐波的性质
我们来看下数字信号中所包括谐波电平的趋势。如果数字信号的电压波形有一个如图6所示的完美梯形波,可以发现几个趋势。
图6(b)显示了梯形波所包括谐波的包络线。如图所示,如果在对数轴上描出频率,谐波的包络线组成一个简单的折线,具有(A,B)两处拐点。[参考文献 2]
A是信号脉冲宽度tp决定的频点。脉冲宽度越窄,A就会越朝向较高频率侧偏移。 B是信号升(降)时间tr决定的频点。此时间段越短,B就会越朝向较高频率侧偏移。(为简化趋势,假设上升和下降时间一致)
(2) 控制谐波电平
谐波的包络线在DC到A点之间(区域a),具有恒定的电平,但在A点至B点之间(区域b)却以20dB/dec(每十倍频率为20dB)的频率速率 下降,然后在B点到较高频率侧(区域c)以40dB/dec的速率急剧下降。因此,从抑制噪声的视点出发,需要将A点和B点向较低频率侧移动。
请参见参考资料[参考文献 2],其阐释了表现这一趋势的理论公式。
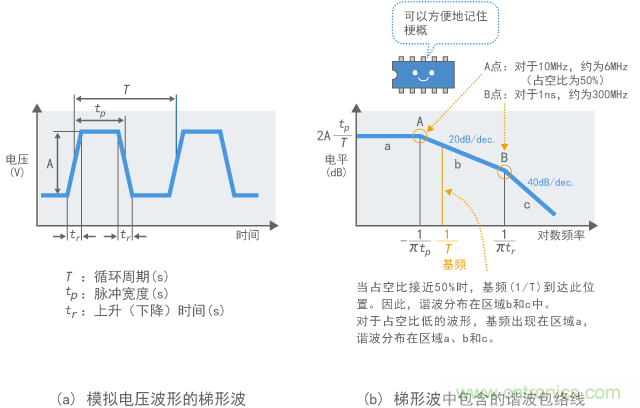
图6 谐波的包络线
(3) 对比理论曲线与实际测量结果
上述频率特性仅表明了一般趋势。各个谐波电平可能受占空循环等因素的影响,而且可能略小于包络线(个别谐波可能非常小)。
图7提供了一个对比图6与实际测量结果的示例。图7 (a)显示了占空比为50%的情况,而(b)显示了占空比为20%的情况。
示波器测量的电压波形显示在图片的左侧,而频谱分析仪测量的频谱显示在中间。观察到了如图1指示的谐波。在图7(b)中占空比为20%的情况下,可以发现偶次谐波的电平几乎等于奇次谐波的电平。
在图片的右侧,中间频谱的频率轴被转换为对数轴,以便与图6中的包络线进行比较。方便您参考,红色线表示理论包络线。可以说,图6的包络 线充分符合频率范围低于100MHz的实际测量结果。在200MHz以上的更高频率范围内,实际测量值小于理论值。这是因为试验中使用的信号发生器因其频 率生成的上限而无法输出精确的梯形波。
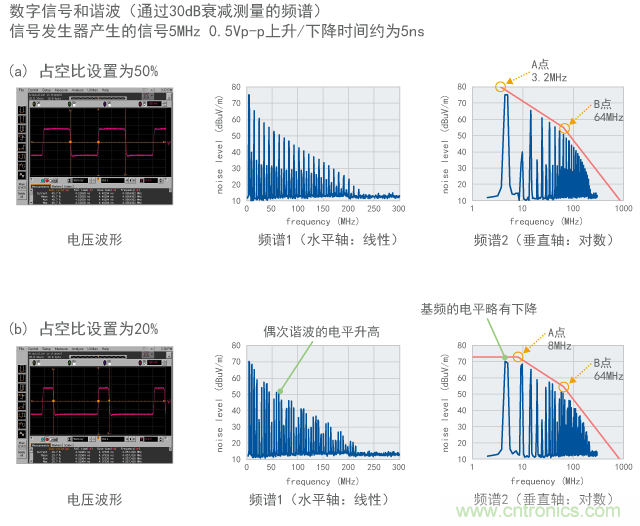
图7 谐波包络线实际测量结果示例
(4) 设计噪声更小的电子设备
以下趋势是从图6(b)所示的包络线形状推导出来的。
(i)信号的循环频率越大,脉冲宽度就越窄。因此,A点向较高频率侧偏移,产生更多噪声。
(ii)随着上升时间变短,信号速度变快,B点朝较高频率侧偏移,产生更多噪声。
要设计噪声更少的电路,应避免这些情况并使A点和B点向低频侧偏移是比较有利的。如果无法在设计中避免上述情况,但信号线附带了安装EMI静噪滤波器的垫子,就更容易抑制噪声了。
当观察实际数字信号的谐波时,难以注意到区域a。这是因为很多数字信号都具有接近50%的占空比,使A点靠近基频的较低频率侧。[page]
信号上升时间的影响
(1) 改变10MHz时钟脉冲信号的上升时间
图6显示了减缓波形上升速度会使B点朝较低频率侧移动,从而抑制谐波电平。图8提供了通过计算确认这个趋势的示例。
此处的谐波是以10MHz循环频率、50%占空比和1V电压大小为基础进行计算的。图片左侧显示了假设的信号波形,中间显示了谐波频谱的计算结果。就像图 7一样,右图显示了将频率轴转换为对数轴的结果。右图以点的形式显示了每个频谱,并叠加了图7所示的包络线。假设使用频谱分析仪测量频谱 电平,并使用有效值进行计算。下列所有数据也同样如此。
(2) B点出现在30MHz处(上升时间为10ns)
图8(a)显示了快速上升的情况(tr =0.1ns),而(b)显示了缓慢上升的情况(tr =10ns)。根据图6中的公式计算出来的包络线B点在条件(a)下大约为3GHz,其明显偏离了图表的显示范围(最大1GHz)。在条件(b)下B点大约为30MHz。 图8(a)的计算结果表明,谐波频谱仅仅是以20dB/dec的速率下降。此外,已经确认在图表的显示范围内(最大1GHz)无法看到B点。
相反,图6(b)的计算结果表明,谐波在30MHz以上的频率范围内以40dB/dec的速率急剧下降。此处附近可能存在一个拐点,即B点。
(3) 在500MHz时下降20dB或更多
相互对比中间的频谱,除了较低频率侧非常小的范围外,其它频率范围内信号上升较慢的(b)的谐波电平变小。在500MHz处相差高达20dB以上。
根据上述计算结果,减缓信号上升速度对抑制谐波很有效。要建立噪声更少的电路,一个有效的方法是在不妨碍电路运作的范围内,选择速度尽可能慢的IC。也可配备信号用EMI静噪滤波器。
对于图8中谐波的计算,使用了村田制作所的EMIFIL®选择辅助工具“MEFSS”。为获得理想的波形,测量条件设定为50Ω。
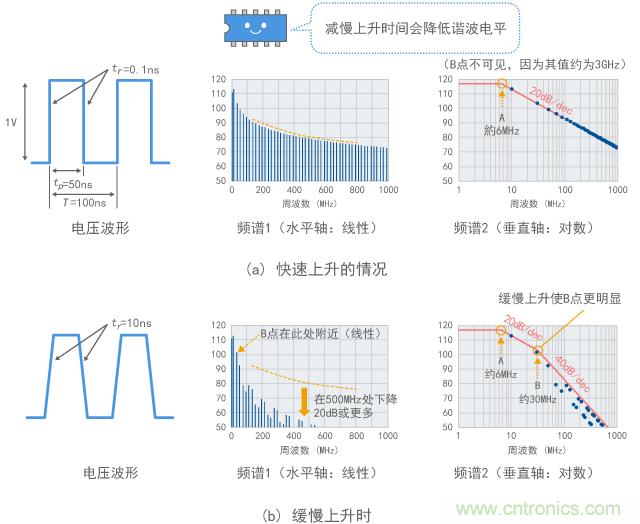
图8 上升速度改变时谐波的变化(计算值)
[page]波形占空比对谐波的影响
(1) 改变10MHz时钟脉冲信号的占空比
时钟脉冲信号是容易产生噪声的一种典型数字信号。时钟脉冲信号通常具有占空比约为50%的波形。如前所述,如果占空比接近50%,信号会包括很强的 奇次谐波,而偶次谐波比较弱。偶次谐波的电平可能随着占空比发生显著变化。(在谐波次数很高的高频范围内,奇次谐波的变化也非常大。)图9提供了 通过计算确认这个趋势的示例。
(2) 谐波分为奇次组和偶次组
此图对比了根据图8(a)所示理想快速上升数字信号将占空比从50%(a)逐渐变为49.9%(b)然后变为49%(c)的谐波。这些计算结果表明,偶次谐波和奇次谐波分别沿着绿色线和黄色线分布,指示偶次和奇次之间存在不同的趋势。
在图9(a)(占空比为50%)中,奇次谐波沿着图6所示的包络线分布,但没有观察到偶次谐波。
(3) 1%的占空比变化可能导致10dB的差别
相反,图9(b)(占空比为49.9%)中显示了偶次谐波,尽管其电平仍然很低。图9(c)(占空比变为49%)显示偶次谐波电平 升高,甚至比特定频率范围内的奇次频率还高。观察1GHz以上的较高频率范围时,或者计算占空比显著偏离50%的情形时,就会发现这样一个趋势: 偶次和奇次谐波电平大小呈周期性切换。请使用MEFSS核实这一趋势。
如上所述,即使是示波器难以辨识的1%占空比变化,也会导致偶次谐波和高次谐波的电平产生几十dB噪声的变化。频谱的一般形状没有太大的变化,仍与图 5所示的包络线一致。但是,单独观察各个频谱时,影响显得很重大。需要注意这种差别,因为这可能导致对噪声测量的再现性产生非常大的影响。
至于如何确定是否符合噪声规定,即使只有一个频谱超过了规定范围,也要视为不符合规定。如果这样的重要变化成分接近于限值,需要仔细地测量。
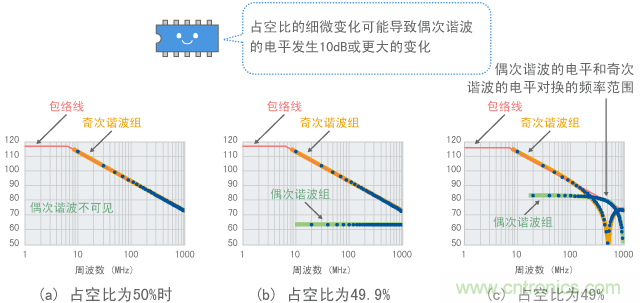
图9 占空比改变时谐波的变化
电压谐波和电流谐波
(1) 比较电压谐波与电流谐波
上述谐波处理方法是以假设电压波形为矩形波为基础的。需要注意的是,即使实际电路的电压波为矩形波,电流波形可能会有所不同。这就意味着,根据噪声是否主要源于电压或电流,噪声发射会呈现出不同的趋势。
图10显示了在假设一个C-MOS数字电路并设有负载为5pF的电容器时,使用MEFSS计算波形和频谱的结果。电压波形接近理想数字脉冲,谐波频谱值接近图6所示的包络线的值(其形状因电容负载而稍有不同,在500MHz左右出现极小点)。[page]
(2) 电流包括更多谐波成分
与电压不同,电流仅在上升和下降瞬间流动,如图所示。如图所示,这样的波形的频谱在高达几百MHz的频率范围内具有恒定的电平(取决于上升时间)。因此,如果因电流出现噪声发射,噪声可能是由高频导致的。这样,MEFSS也能计算电流波形的频谱。
在如图2-3-14所示的噪声测量结果中,(b)中500MHz以上几乎没有任何电压频谱,而(c)中的发射噪声频谱显示出了强烈的发射。因此,我们可以 看到如此噪声源和发射噪声间的频率分布有一定差异,其原因之一就是此次试验中发射噪声是由电流引起的。(除了本试验之外,也存在电压为噪声发射的起因)
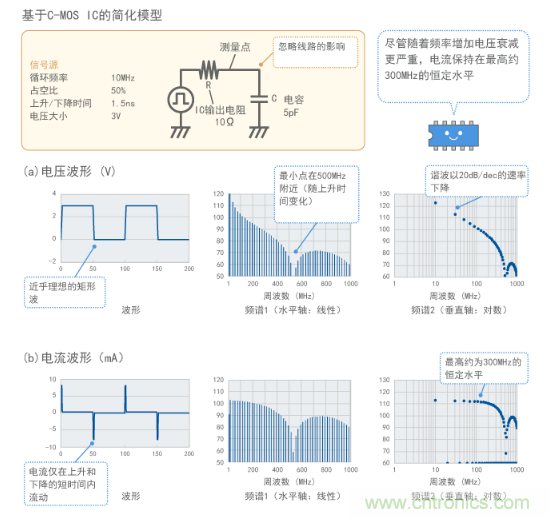
图10 电压和电流之间的区别
(3) 电流有一个长钉一样的峰值波形
如果您认为图10中因为电流波形为细小的长钉形状,那么电流谐波未在高频率范围内衰减的原因是可以理解的。考虑到图6中的梯形波, 长钉形的波形,就像电流波形,可以被视为占空比非常小时的梯形波模型。对于占空比较小的梯形波的包络线,A点向高频率侧偏移,在很高频率范围内保持恒定的 电平。因此,可以观察到当前波形的谐波持续到很高频率而不会衰减。请注意,图6中的梯形波模型不同于当前波形,因为当前波形的长钉指向上方和下方。因此,当移动A点时,占空比较小的梯形波模型具有更强的谐波。但是,这一趋势在当前波形中比较弱。[page]
谐振产生的脉冲波形变化的影响
(1) 谐振导致脉冲波形失真
由于上述阐释假设数字信号脉冲波形是理想的矩形波,如果波形因电路状况而偏离了矩形波,则需要进行修正。脉冲波形失真的其中一个原因在于驱动器IC、接收器IC和线路的谐振。本章节讲述谐振导致波形失真时频谱的变化。
如果忽略线路的影响,C-MOS数字电路可以视为如图10模型图所示的非常简单的电路,用于在模拟中获得理想的脉冲波形。
(2) 因线路长振铃导致噪声增加的示例
如果将线路的影响加入此电路,波形会是什么样的?计算结果如图10所示。图11对比了有线路电路和无线路电路的波形,其中假设线路 长达20 cm,以使波形变得明显。如果有线路,信号波形出现很大的振铃。相应地,会发现在约150MHz处谐波出现显著上升的趋势。(为了观察振铃,在比图 10更宽的范围内测量了电压)
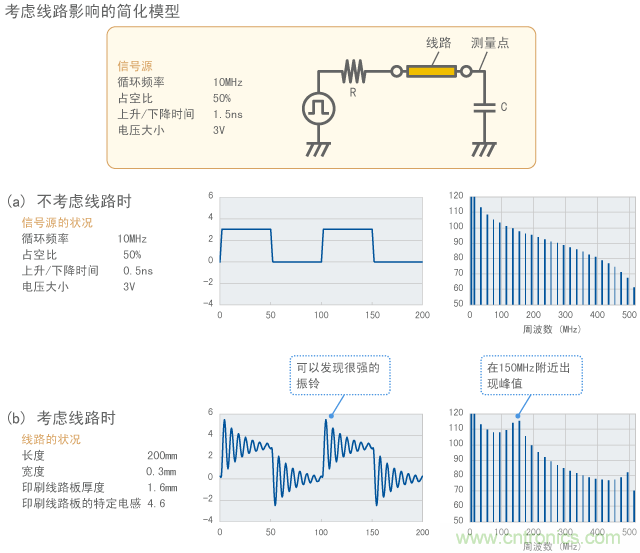
图11 线路的影响导致振铃
(3) 通过试验确认振铃
在实际数字电路中经常看到这样的振铃。图12显示了一个测量结果示例,其中连接了一根20 cm的导线。尽管不如图11中模拟结果那么强烈,振铃还在以相似循环出现,显示出在150MHz左右谐波显著增加的趋势。因此,如果数字电路连接 了一根更长的信号线,信号波形更可能遭受振铃影响。在这种情况下,振铃频率可能导致更高的谐波电位,进而造成噪声问题。
图12中测量结果的振铃相对而言小于图11中测量结果的振铃。这是因为实际电路在IC和线路中多少有些损耗,造成了短时间的衰减。电压也更低,低于图12中的3 V。此外,测量时使用频带2.5GHz的FET探针作为电压探针,其电压比为10:1。因此,图12所示的频谱值为20dB,低于实际值。
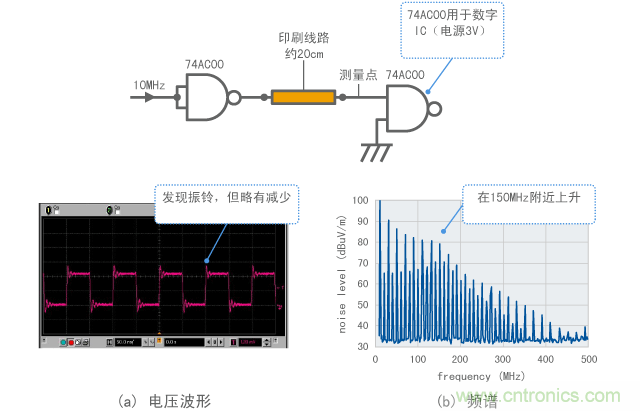
图12 观察示例(测量的振铃)
(4) 线路中的电感导致谐振,进而形成振铃
图11所示的振铃是因线路电感在信号电路内形成的谐振电路的结果。图13(a)为模型图。
在图13(a)中记录了线路中微小的电感和静电容量。通过这种方式可以了解到信号电路中创建了一个RLC串联谐振电路。
当放大图11信号上升部分中产生的振铃时,可以发现循环周期约为7ns的阻尼震荡波形,如图13(b)所示。7ns的循环周期等同于143MHz频率,几乎与图11中观察到的上升谐波的频率(150MHz)一致。[page]
(5) 线路中有多少电感?
根据传输理论指示的单位长度参数,图11中所假定20 cm导线的电感和静电容量的计算结果分别为约140nH和10pF。如果将这些值应用于图13(a)中的RLC串联谐振电路,谐振频率估计为 110MHz左右。尽管这个结果比图11中观察到的150MHz小30%,但还是基本一致,因此图13(a)中的简化模型与理解振铃机制 有关。
如果需要更精确地估计谐振频率,需要将线路作为传输线而不是使用电感和静电容量等集中参数。(请参考技术文档,查阅如何计算线路的单位长度参数及如何将线路作为传输线[参考文献 5,6,7])
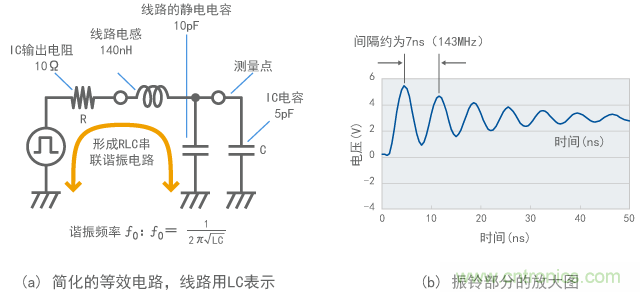
图13 振铃的起因
(6) 通过铁氧体磁珠吸收振铃
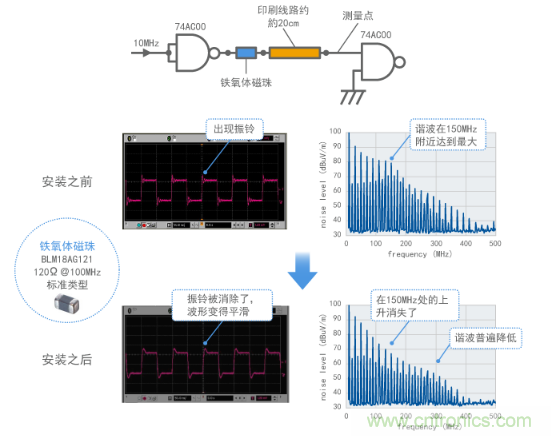
通常,为了抑制谐振,要使用阻尼电阻器。如果想同时减少噪声,则有效的方法是使用铁氧体磁珠替代阻尼电阻器。图14显示了在之前模型中使用铁氧体磁珠的计算结果。此外,图15显示了在图12中使用的测试电路中使用铁氧体磁珠的计算结果。
由于图14和图15中连接了铁氧体磁珠,振铃已经被消除了,150MHz左右的谐波升高也消失了,且同时也降低了500MHz以下整个频 率范围中的谐波电平。通过这种方式,铁氧体磁珠能够有效抑制谐振和不需要的谐波。铁氧体磁珠已经广泛用于消除数字信号谐波造成的噪声。

图14 通过铁氧体磁珠抑制振铃(计算结果)
[page]通过EMI静噪滤波器消除谐波
(1) EMI静噪滤波器消除能够导致噪声的谐波
使用EMI静噪滤波器(如铁氧体磁珠等)可以彻底消除数字电路中不需要的谐波,从而抑制来自谐波的噪声。EMI静噪滤波器及其使用方法将在单独的章节中进一步讲述;本章仅提供一个关于其作用的示例。
尽管可以通过使用慢速IC(如前所述)或者电阻器等通用部件减缓上升时间,进而在一定程度上实现抑制谐波,但使用EMI静噪滤波器能过获得更多效果。即使信号波形看起来相同,但噪声抑制效果还是可能有10dB或更多的区别。
(2) 使用20MHz时钟脉冲信号的50MHz截止滤波器
图16显示了使用EMI静噪滤波器消除20MHz时钟脉冲发生器噪声的试验示例。在此对比了使用三端子电容器的情形和使用截止频率为50MHz的π型滤波器(具有急剧变化的频率特征)的情形。尽管两种情况下的减噪效果都很出色,但可以发现信号波形的变化和上升时间并不一定与噪声抑制效果相符。π型滤波器似乎能够在保持脉冲式信号波形和上升时间的同时消除噪声。
(3) 示波器或频谱分析仪上的噪声看起来不一样
这是因为相对较低的频率成分在单个波形中比较显眼,而相对较高的频率成分在噪声测量中比较显眼。由于单个波形的观察结果显示了所有频率相加之后的波 形,幅值较大的低次谐波会施加更强烈的影响。相反,噪声测量离散地观察每个频率,而且由于其容易由更小的天线发射,更多地受到了高(高次)频率的影响。
(4) 用于信号的EMI静噪滤波器
如果使用具有急剧频率变化特征的滤波器,就像图16所示π型EMI静噪滤波器,就能在保持信号质量的同时有效抑制噪声。这种EMI静噪滤波器将在后续章节中进一步讲述。

图16 通过EMI静噪滤波器消除谐波的示例





