【导读】在当今计算技术快速发展的浪潮中,模拟计算作为一种独特的计算范式,正日益彰显其特有的吸引力与潜力。与依赖离散数字信号的传统数字计算不同,模拟计算直接运用物理定律,借助连续变化的物理量(如电压、电流等)来完成计算任务。这种计算方式在能效和速度上具有明显优势,因为它绕过了数字计算中繁琐的数模转换步骤,能够更直接、高效地处理信息。近年来,随着人工智能硬件领域的迅速兴起,模拟计算凭借其高效能特性,受到了广泛的关注和深入研究。
在模拟计算的广泛范畴内,模拟存内计算作为一项新兴技术,已成为当前研究的热点。其核心理念是将计算与数据存储深度融合,直接在存储单元内部完成计算操作,从而大幅减少数据在存储与计算单元之间的搬运次数,显著提升了计算效率并降低了能耗。这种计算模式尤其适合需要处理海量数据的应用场景,如神经网络推理和图像处理等,为人工智能硬件的发展开辟了新的路径。然而,尽管模拟计算与模拟存内计算具备诸多优点,目前仍普遍面临计算精度不高、稳定性不足的挑战。这主要是因为现有模拟硬件方案高度依赖于器件本身的物理参数(如电阻值),而这些参数在编程过程中往往存在较大的随机偏差,且容易受温度等环境因素干扰。上述特性限制了模拟计算精度的提升,成为制约其实际应用的关键瓶颈。
最近,南京大学物理学院缪峰教授与梁世军教授课题组针对这一难题,提出了一种高精度模拟计算方案,为模拟存内计算领域带来了重要突破。该方案将模拟计算权重的实现方式,从易受干扰、不稳定的物理参数(如器件电阻)转向高度稳定的器件几何尺寸比例,从而突破了制约模拟计算精度的主要障碍。
基于这一创新思路,研究团队设计并验证了一款采用标准CMOS工艺的模拟存内计算芯片。结合权重重映射技术,该芯片在并行向量-矩阵乘法运算中实现了仅0.101%的均方根误差,创造了模拟向量-矩阵乘法运算精度的最高纪录。值得一提的是,该芯片在-78.5°C和180°C的极端温度条件下仍能稳定工作,矩阵计算的均方根误差分别保持在0.155%和0.130%,显示出在极端环境下维持高计算精度的卓越能力。此外,该方案还可适配多种二值存储介质,具备广泛的应用前景。
本研究的核心思路是将模拟计算权重的实现基础从器件参数转向器件的几何比例(图1A),利用器件几何比例在制备完成后高度稳定的特性,实现高精度计算(图1B)。基于该思路,团队通过电路拓扑设计,结合存储单元和开关器件,构建了可编程的计算单元(图1C)。该单元通过两级依赖尺寸比例的电流拷贝电路,实现输入电流与8比特权重的乘法运算:第一级的几何比例由8位存储器控制;第二级为固定比例,为不同列上的第一级输出电流赋予对应的二进制权重。两级共同作用,决定了计算单元的整体等效比例,从而实现权重可编程的模拟乘法运算。通过将这些计算单元以阵列形式排布,团队成功设计出一款高精度电流域向量-矩阵乘法芯片(图1D)。
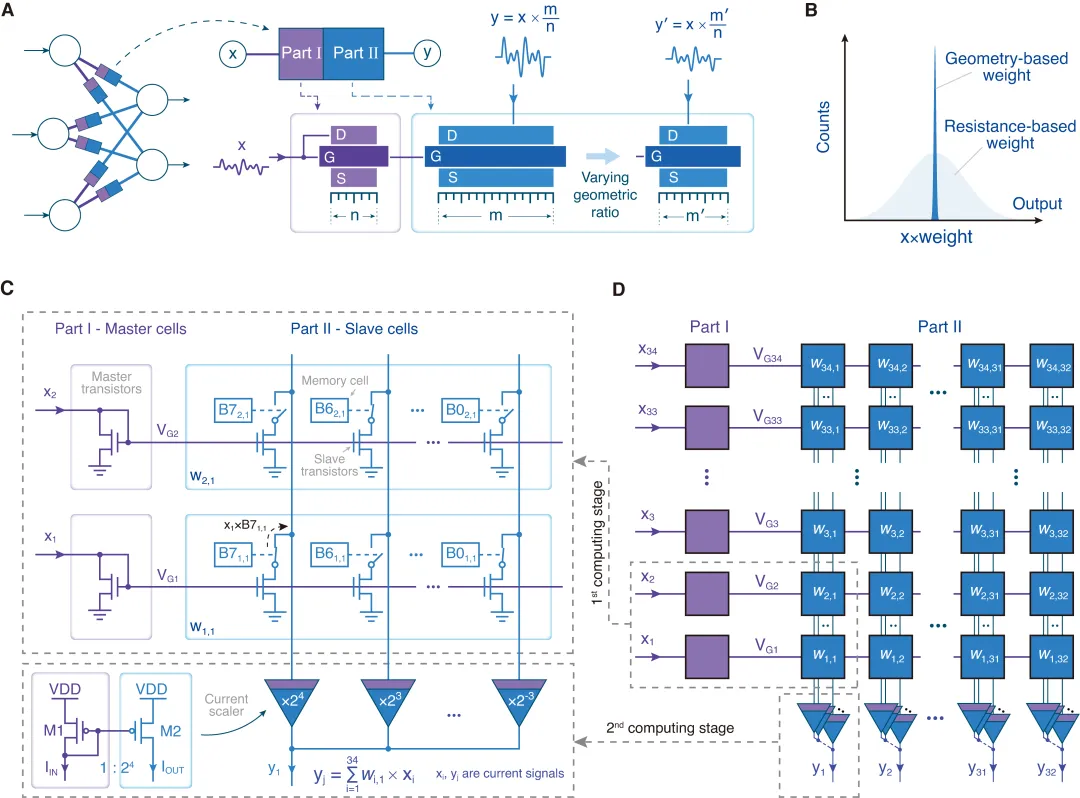
图1:高精度模拟计算方案与电路结构。(A) 概念示意图。本方案利用器件的物理尺寸决定模拟信号的运算关系。(B) 实现效果示意图。利用器件物理尺寸的稳定性,本方案可实现超越传统方案的计算精度。(C) 计算单元原理图。通过两级依赖尺寸比例的电流拷贝电路设计,结合存储单元和开关器件,构建了等效尺寸比例可编程的计算单元,实现输入电流与8比特权重的模拟乘法运算。(D) 计算阵列原理图。通过阵列化排布计算单元,设计高精度电流域向量-矩阵乘法芯片。
随后,研究团队基于180nm CMOS工艺对该方案进行了流片验证。芯片照片与测试电路如图2A所示。团队通过执行多轮随机向量-矩阵乘法,全面测试了芯片的计算精度。测试所用矩阵规模为64×32(图2B),由4块芯片共同组成。同时,团队提出了一种权重重映射方法(图2C),能够充分利用器件尺寸比例的稳定性,进一步提高芯片的计算精度。在1500次随机向量-矩阵乘法实验中,芯片的实际输出结果与理论值几乎完全吻合(图2D),显示出极高的计算精度。进一步的统计分析表明,芯片计算相对误差的均方根仅为0.101%(图2E),刷新了模拟计算领域的最高精度纪录。与其他先进模拟计算方案相比,本芯片的计算精度显著提升(图2F)。
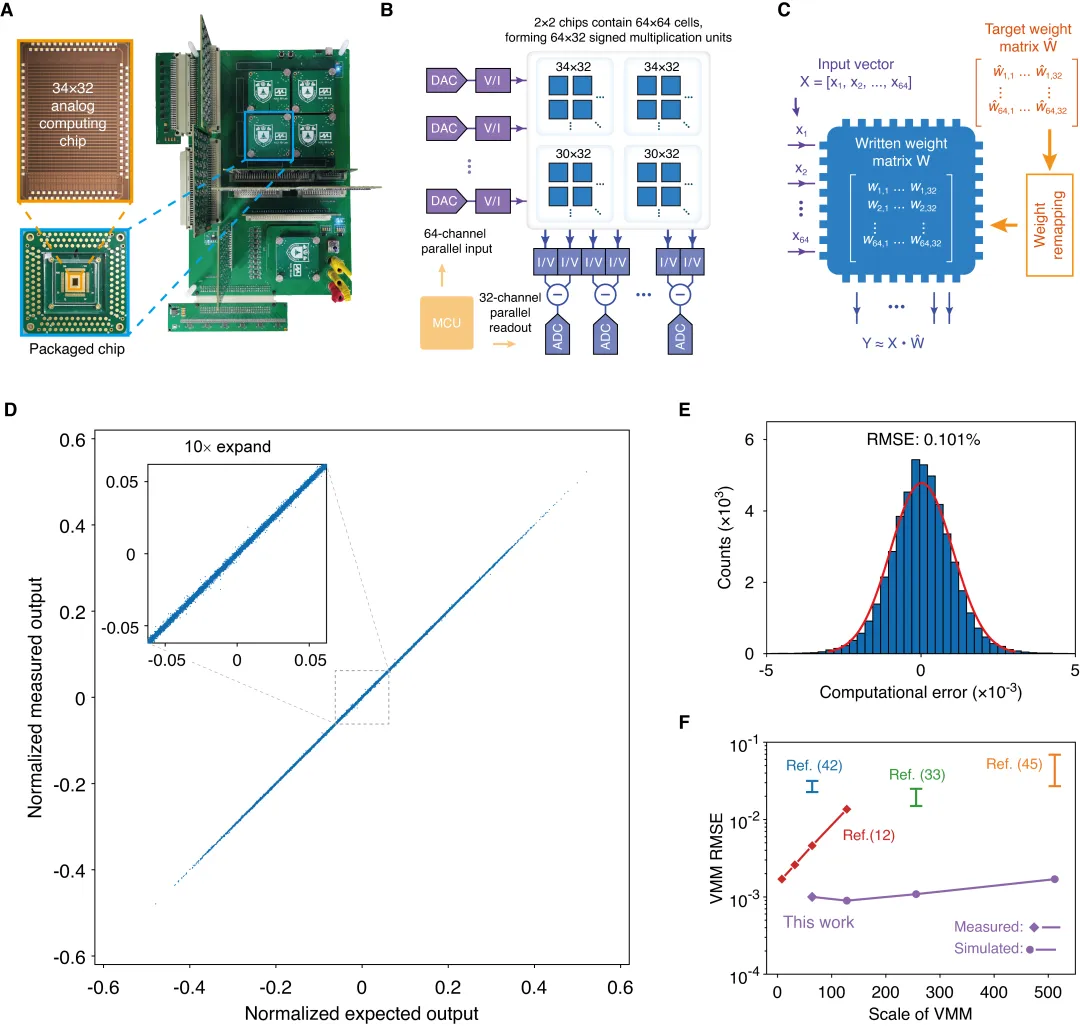
图2:高精度模拟向量-矩阵乘法测试。(A) 芯片和测试电路照片。(B) 模拟向量-矩阵乘法精度测试电路原理图。(C) 权值重映射方法示意图。该方法能进一步提高芯片计算精度。(D) 1500组随机向量-矩阵乘法结果。理想输出与实际输出几乎重合。(E) 归一化计算误差的分布图,统计得其均方根仅为0.101%。(F) 本芯片与其他先进模拟计算方案的精度对比。
该芯片所具备的超高模拟向量-矩阵乘法精度,使其在实际任务中表现卓越。研究团队首先测试了芯片在神经网络推理任务中的效果:利用该高精度模拟存算芯片执行图3A所示神经网络中的所有卷积层和全连接层运算,在MNIST测试集上的识别准确率达到97.97%(图3C),与64位浮点精度下的软件识别结果相近(仅相差-0.49%),并显著优于传统模拟计算硬件(提升+3.82%)。进一步,团队评估了芯片在科学计算中的表现,利用该芯片求解纳维–斯托克斯方程以模拟流体流动行为。实验结果显示,芯片计算得到的流体运动状态(图3D)与64位浮点精度下的软件结果高度一致(图3E),而传统低精度模拟计算硬件在相同任务中则无法得出正确结果(图3F)。
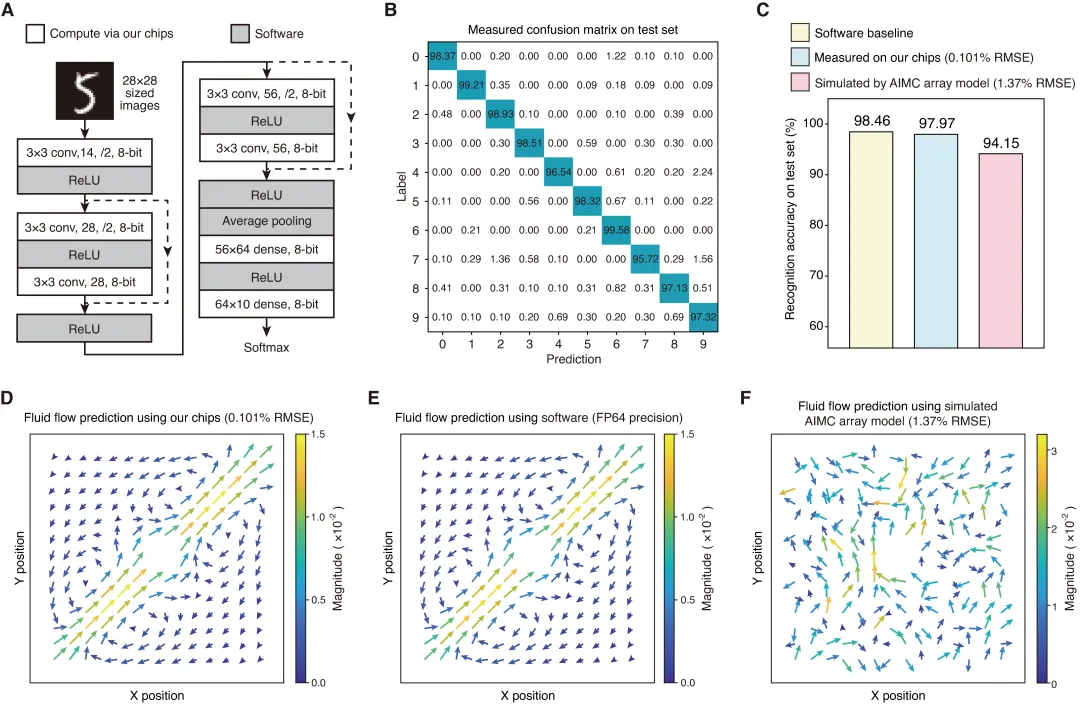
图3:高精度模拟计算芯片的应用表现。(A) 神经网络结构与数据集。(B) 在MNIST测试集上识别结果的混淆矩阵,识别率达到97.97%。(C) 准确率对比。高精度模拟计算芯片测试结果与64位浮点精度下的软件识别率相近(-0.49%),显著优于传统模拟计算硬件(+3.82%)。(D) 高精度模拟计算芯片求解纳维–斯托克斯方程得到的流体行为预测结果。(E) 64位浮点精度下的软件计算结果,本芯片结果与其高度一致。(F) 低精度模拟计算硬件的结果无法准确反映流体行为。
研究团队不仅验证了该模拟存算芯片的超高计算精度,还测试了其在极端环境下保持计算精度的鲁棒性。即便在外部环境变化的情况下,器件的几何比例仍能保持恒定,使芯片在极端条件下依然维持较高的计算精度。团队在-78.5℃和180℃的环境下执行模拟向量-矩阵乘法测试,测得相对误差的均方根分别仅为0.155%和0.130%(图4A、B)。在更宽温度范围(-173.15℃至286.85℃)的测试中,芯片核心单元的输出电流相对于常温条件的最大偏差仅为1.47%(图4C-F)。此外,团队还在强磁场环境(最高10T)中对芯片输出电流进行了测量,结果显示,芯片核心单元的输出电流相较于无磁场条件的变化不超过0.21%(图4G-J)。以上结果充分证明了该高精度模拟计算方案在极端环境下的可靠性。
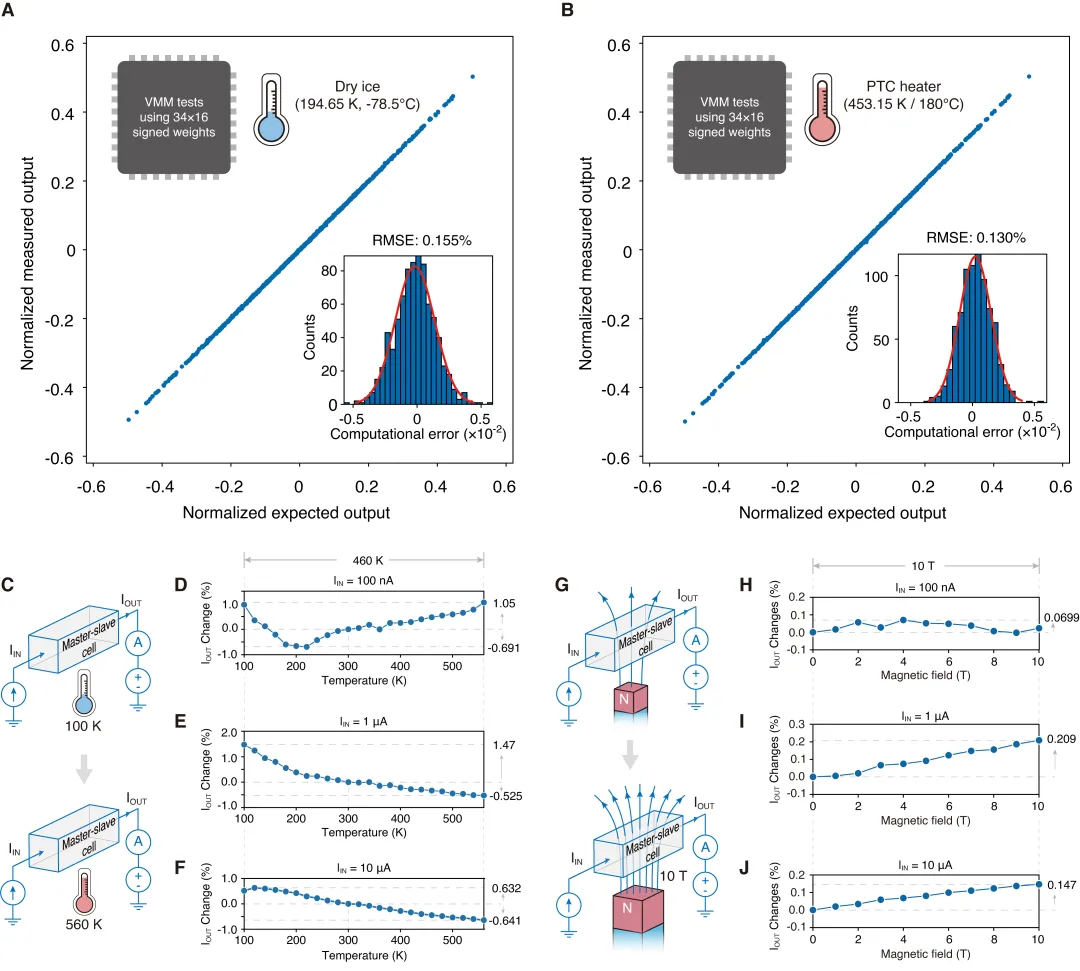
图4:高精度模拟计算芯片的鲁棒性测试。(A) 低温下(-78.5℃)芯片的向量-矩阵乘法精度测试结果。测得芯片输出的相对误差均方根为0.155%。(B) 高温下(180℃)芯片的向量-矩阵乘法精度测试结果。测得芯片输出的相对误差均方根为0.130%。(C) 将芯片核心单元置于更宽温区(-173.15℃至286.85℃)进行测试的示意图。(D)-(F) 宽温区下的输出电流测量结果。相对于常温条件,输出电流偏差不超过1.47%。(G) 将芯片核心单元置于强磁场(最高10T)下进行精度测试的示意图。(H)-(J) 强磁场下的输出电流测量结果。相对于零磁场条件,输出电流偏差不超过0.21%。
相关研究成果以“Ultrahigh-precision analog computing using memory-switching geometric ratio of transistors”(基于器件尺寸比例稳定性的超高精度模拟计算方案)为题,于2025年9月12日发表在学术期刊《Science Advances》上。







