在某些应用中，若整个时间范围内作用于系统的净加速或力是重力，那么可以使用加速度计来测量倾斜的静态角度。这类应用有：游戏机、相机中的水平检测，以及在工业和医疗应用中检测设备的驶向。

 

对于采用加速度计的倾斜检测，假设重力是唯一的加速激励因素。在实际使用中，可在信号输出端执行信号处理，移除输出信号的高频成分，因此一定程度的交流加速度是可以接受的。

 

倾斜检测利用重力矢量及其在加速度计轴上的投影来确定倾斜角度。由于重力是直流加速度，任何产生额外直流加速度的力均会破坏输出信号，导致计算错误。直流加速度的来源包括车辆在一定时间内以恒定速度加速，以及旋转器件在加速度计上产生向心加速度。此外，通过重力旋转加速度计，随着目标轴上的重力投影变化，会引起明显的交流加速度。在计算倾斜之前，对加速度信号进行任何形式的滤波都会影响建立输出新静态值的速度。

 

本应用笔记讨论将加速度计输出转换为倾斜角度的基本原理。讨论内容包括如何计算单轴、双轴或三轴解决方案的理想倾斜角度。此外还包括一些关于校准的基本信息，以减少失调和灵敏度失配所引起的误差。

 

倾斜计算

 

单轴倾斜计算

 

在只需对有限的角度范围内进行倾斜检测的应用中(该应用的分辨率精度较低)，可使用单轴器件(或多轴器件中的单个轴)。

 

例如，在图1中，单轴(本例中是x轴)通过重力旋转。由于此方法仅使用单轴，且需要重力矢量，因此只有当器件的x轴始终位于重力平面上时，倾斜计算角度才是精确的。其他轴上的任何旋转都会降低加速度在x轴上的幅度，计算倾斜角度时便会产生误差。

 

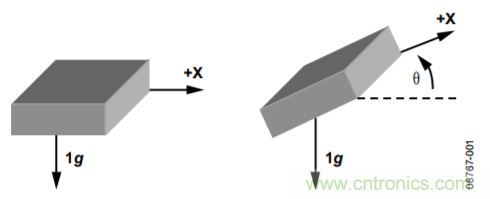
图1. 用于倾斜检测的单轴

 

根据基本三角恒等式，x轴上的重力矢量投影会产生输出加速度，大小等于加速度计x轴和水平面之间夹角的正弦值。水平面通常是与重力矢量正交的平面。当重力为理想值1 g时，输出加速度为：

 

 

使用单轴解决方案时——也就是说，输出的变化引起输入的某些变化——倾斜计算随着水平面与x轴夹角的增加而下降，当夹角接近±90°时，数值接近0。这点可以从图2中看出，其中绘出了输出加速度(以g表示)与倾斜角之间的关系图。接近±90°时，倾斜角出现很大变化时，输出加速度只会产生很小变化。

 

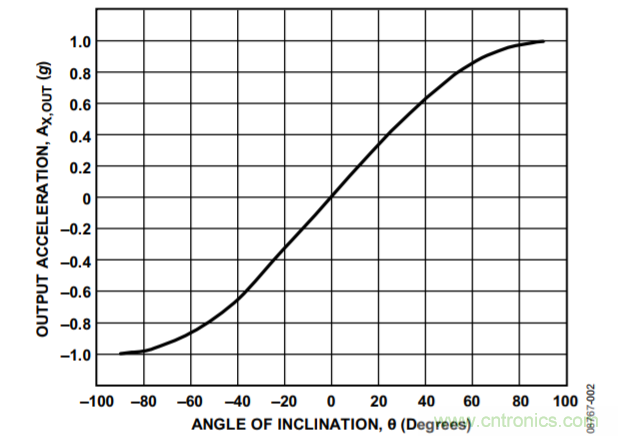
图2. 输出加速度与倾角的关系(单轴倾斜检测)

 

由于以数字化的方式执行倾斜计算，输出加速度根据最低有效位(LSB)或代码表现为恒定加速度，并由模数转换器(ADC)获取，或者直接从数字输出部分获取。由于输出分辨率是恒定的加速度，倾斜分辨率(以度为单位)是可变的，其最佳分辨率接近0°，最差分辨率为±90°。

 

图3和图4显示倾角步进为1°和0.25°时的增量灵敏度。增量灵敏度等于输出变化，以mg显示，表示每个倾角的步进，或者：

 

 

其中：

 

N为当前角度。

 

P为步长。

 

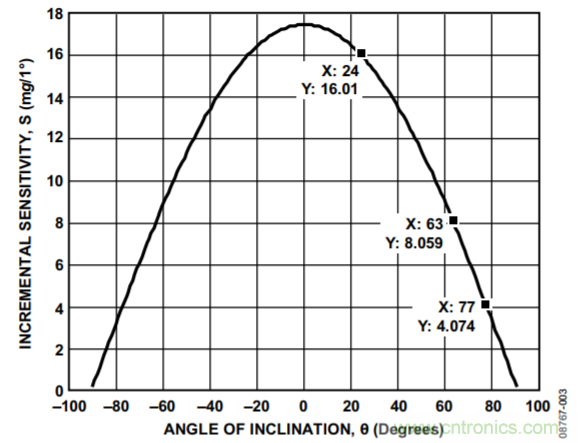
图3. 步进为1°时的增量倾斜灵敏度

 

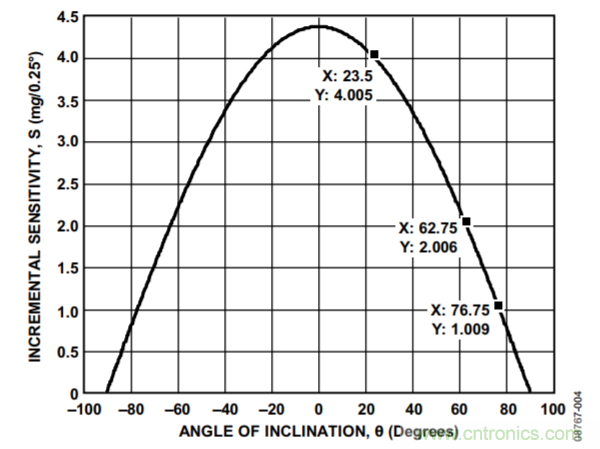
图4. 步进为0.25°时的增量倾斜灵敏度

 

测量输出加速度时，为了满足应用在整个范围内所需的倾斜分辨率，可利用这些曲线确定需达到的最小分辨率。例如，设计最大步长为1°，则针对±63°范围，分辨率至少需达到8 mg/LSB。类似地，为达到±63范围内的0.25°最大步长，则分辨率至少为2 mg/LSB。请注意，如果存在较大的扰动，可以使用过采样以获得更佳分辨率。

 

通过重力旋转时，由于加速度计输出符合正弦关系，使用反正弦函数可以将加速度转换为角度。

 

 

其中，倾斜角θ单位为弧度。

 

如果需要窄范围倾斜，可以使用线性近似法取代反正弦函数。线性近似与小角度正弦近似有关。

 

 

其中，倾斜角θ单位为弧度。

 

额外的比例系数k可用于倾角的线性近似计算中，若容许的误差有所增加则可扩大近似的有效范围。

 

 

其中，倾斜角θ单位为弧度。

 

将等式5的结果乘以(180/π)，可转换为度。图5显示使用反正弦函数与使用k = 1时线性近似的对比。随着倾角幅度的增加，线性近似开始下降，计算得到的角度与实际角度发生偏差。

 

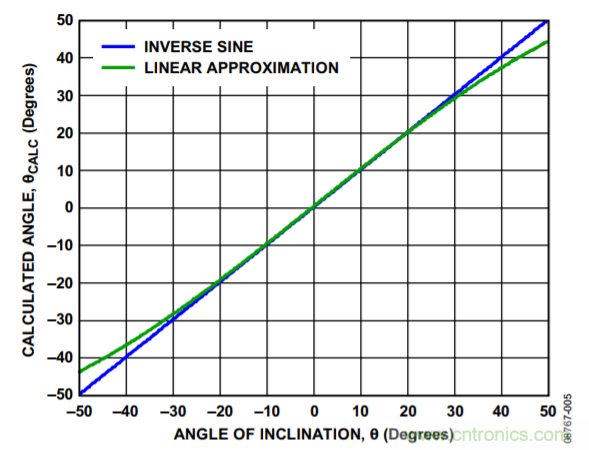
图5. 倾角计算中反正弦函数与线性近似的对比

 

由于计算角度根据实际倾角绘制，因此线性近似在靠近尾部时开始弯曲。这是因为线性近似仅在对比输出加速度时才表现为线性，如图2所示。随着倾角增加，输出加速度的表现与之相似。然而，反正弦函数应当产生与实际倾角一对一对应的输出，从而当描绘实际倾角时，计算得到的角度为一条直线。

 

例如，假设倾斜检测所需的分辨率为1°，则±0.5°的误差是可以接受的，因为它低于计算的舍入误差。若在k = 1的情况下绘制实际倾角与计算倾角之间的误差(如图6所示)，则线性近似的有效范围仅为±20°。若比例系数经调节后，使得误差最大但依然保持在计算得到的舍入限值内，则线性近似的有效范围增加到±30°以外。

 

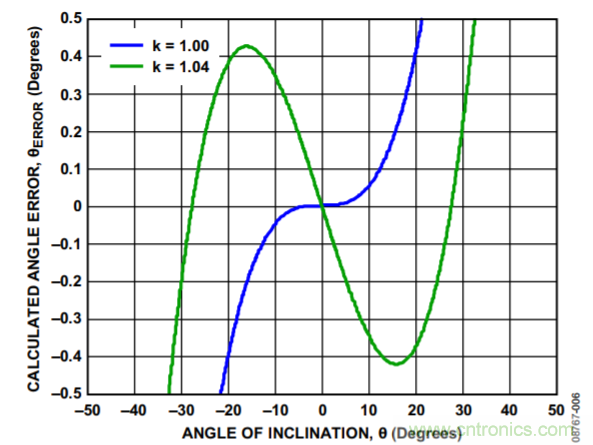
图6. 不同比例系数下计算得到的角度误差

 

双轴倾斜计算

 

单轴倾斜检测的一个限制，是需要高分辨率ADC或数字输出来实现大范围的有效倾角，如图3和图4所示；另一个限制，是单轴测量无法提供360°的测量，因为在倾角N°时产生的加速度与倾角180° − N°时产生的加速度相同。在某些应用中，这是可以接受的；但对于需要更高分辨率或要求在完整的360°弧度范围内区分倾角的应用而言，则需要第二条轴(如图7所示)，或者需要第二个传感器。若使用了第二个传感器，则其朝向应使第二个传感器的检测轴与第一个传感器的检测轴相互正交。

 

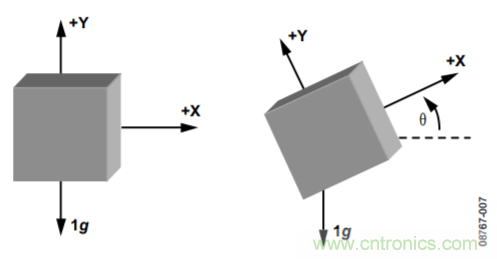
图7. 用于倾斜检测的双轴

 

增加一个轴对确定倾斜角有三大好处。下文说明这些好处。

 

恒定灵敏度

 

增加一个轴的第一大好处在于两个轴相互垂直。与单轴解决方案相同，x轴检测到的加速度与倾斜角的正弦值成比例。由于两个轴相互垂直，因此y轴加速度与倾斜角的余弦值成比例(见图8)。随着一条轴的增量灵敏度下降(比如该轴的加速度接近+1 g或−1 g)，另一条轴上的增量灵敏度将会上升。

 

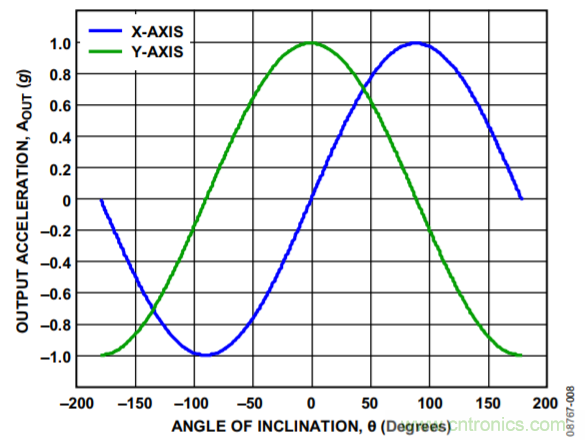
图8. 输出加速度与倾角的关系(双轴倾斜检测)

 

将测量的加速度转换为倾角的一种方法，是计算x轴的反正弦函数和y轴的反余弦函数，与单轴解决方案类似。但是，更简单有效的方法是使用两个数值之比，可得到如下结果：

 

 

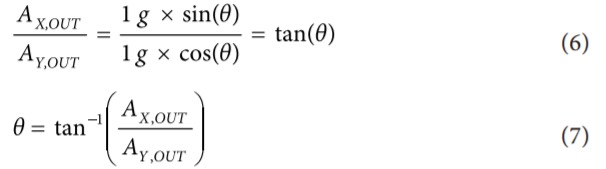
其中，倾斜角θ单位为弧度。

 

与单轴示例不同，使用两轴之比来确定倾角会使得增量灵敏度的确定变得十分困难。相反，假设所需的倾斜分辨率已知，则确定加速度计需达到的最低分辨率用处更大。假定一条轴的增量灵敏度随着另一条轴的增量灵敏度下降而上升，则净结果将是数值基本恒定的有效增量灵敏度。这表示若针对某一角度，为达到所需的倾斜步长要求而选择加速度计，则该加速度计将具备足够的分辨率以应付所有角度。

 

为确定所需的最小加速度计分辨率，可检查等式6，确定分辨率的极限。由于每条轴的输出和倾角的正弦或余弦有关，并且每种函数的倾角均相同，因此可求解的最小角度与可求解的最小加速度有关。

 

如图3和图4所示，正弦函数在0°附近具有最大速率变化，且可以看出，余弦函数在该点处具有最小速率变化。由于这个原因，倾斜导致的x轴加速度变化将先于y轴加速度变化而被识别。因此，系统在0°附近的分辨率主要取决于x轴的分辨率。如需确定P°的倾斜变化，加速度计必须要能检测根据下式所确定的变化量近似值：

 

 

对于所需的倾斜步长，图9可用来确定所需的最小加速度计分辨率(或最大加速度计比例因子)。注意，加速度计分辨率的提升不仅与加速度计比例因子的降低有关，还与检测更小的输出加速度变化的能力有关。因此，针对目标倾斜步长选择具有适当分辨率的加速度计时，比例因子应当小于图9所示的限值。

 

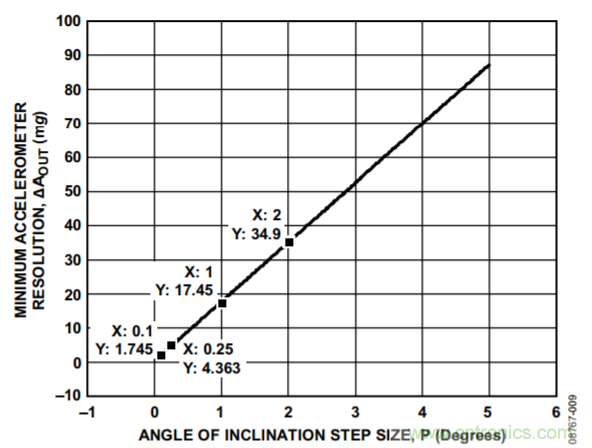
图9. 用于目标倾角分辨率的最小加速度计分辨率

 

降低与重力平面对齐的依赖性

 

使用至少两个轴的第二大好处是，与单轴解决方案不同，增加一个轴后，即使第三个轴上存在倾斜，也可以测出精确值。而在单轴解决方案中，只要除x轴以外的任何其它轴上存在倾斜，就会造成显著误差。这是因为有效增量灵敏度与目标轴上重力的和方根(RSS)值成比例。

 

若重力完全包含在xy平面中，那么在理想情况下，那些轴上检测到的加速度RSS值等于1 g。若在xz或yz平面上存在倾斜，则重力导致的总加速度将下降，从而降低有效增量灵敏度。这样会增加给定加速度计分辨率的倾斜步长，但依然可以提供精确的测量结果。倾角计算结果与xy平面上的旋转有关。

 

若系统足够倾斜，以至于xy平面上只有极少量由于重力而造成的加速度，那么倾角步长将会分辨率过低而不可用；因此，建议限制xz或yz平面的倾斜程度。

 

完整360°倾斜检测

 

增加一个轴的第三大好处是，能够区分各个象限并在整个360°弧度范围内测量角度。如图10所示，每个象限都具有与x和y轴加速度关联的不同符号组合。

 

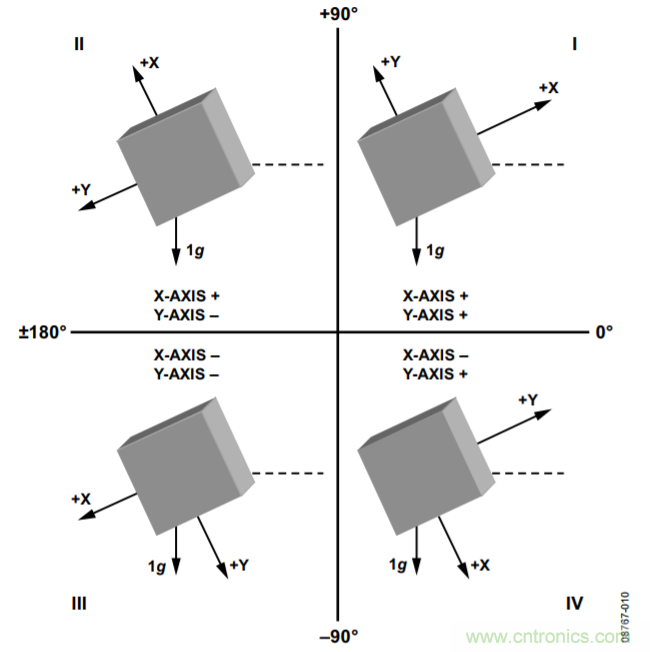
图10. 象限检测的倾角和加速度符号

 

如果操作数AX,OUT/AY,OUT为正值，反正切函数会返回第一象限中的值；如果操作数为负值，则反正切函数会返回第四象限中的值。第二象限内的操作数为负值，因此在计算该象限内的角度时应将结果加上180°。第三象限内的操作数为正值，因此在计算该象限内的角度时应从结果中减去180°。而该角度所处的确切象限则可以通过各轴上测得的加速度符号来确定。

 

三轴倾斜计算

 

引入第三条轴后，便可在全部范围内确定传感器。经典的矩形(x, y, z)到球形(ρ, θ, φ)转换方法可将xy平面的倾角θ以及重力因素产生的倾角φ与每条轴上的测量加速度相关联，如下所示：

 

 

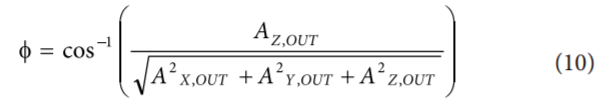
假设重力是唯一测得的加速度原因，则等式10分母上的操作数可以常数代替(最好是1)，因为此时所有轴上的RSS值为常数。角度如图11所示；图11c显示θ只在xy平面上存在，而图11d显示φ为z轴与重力矢量之间的夹角。

 

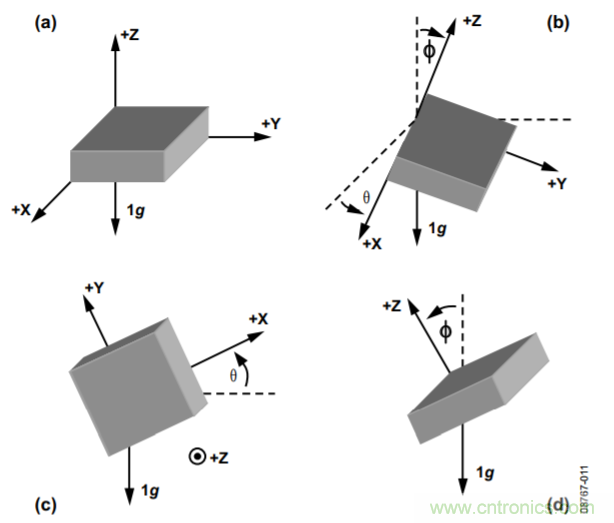
图11. 球形坐标系统的角度

 

由于三轴法与单轴/双轴法具有相似的等式，因此三轴解决方案的分析与单轴和双轴法结合使用时相同。两条正交轴之比有助于θ的测量，并且要达到要求的倾斜分辨率需要具备一个最小加速度计分辨率，如等式8所示。

 

φ的测量不仅与单轴解决方案的倾角测量有关，还与目标范围内实现特定倾角分辨率所需的最小加速度计分辨率的确定有关。区别在于，使用反余弦函数确定φ会使φ在90°时具有最大的增量灵敏度，而在0°和180°时具有最小的增量灵敏度。

 

以余弦代替等式2中的正弦，即可产生类似图3和图4的曲线。重要的是需注意，虽然θ的范围为−180°至+180°，但φ的范围仅为0°至180°。若φ的角度为负数，则θ的角度也会变为负数。

 

三轴倾斜检测的一种替代方法是单独确定加速度计每条轴与参考位置之间的夹角。参考位置通常选择器件的x轴和y轴位于水平面的方向上(0 g场)，并且z轴与水平面垂直(1 g场)。图12显示该方法，其中，θ表示水平面与加速度计x轴之间的夹角，ψ表示水平面与加速度计y轴之间的夹角，φ表示重力矢量与z轴之间的夹角。当位于x和y轴的0 g以及z轴的1 g初始位置时，所有计算的角度均为0°。

 

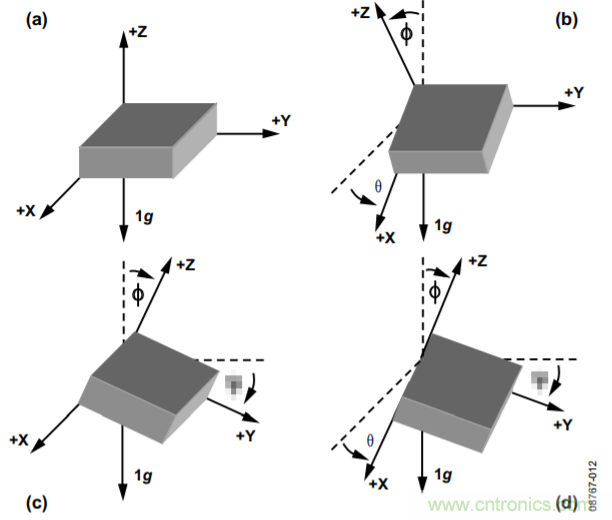
图12. 独立倾斜检测的角度

 

可利用基本三角恒等式计算倾角，如等式11、12和13所示。

 

 

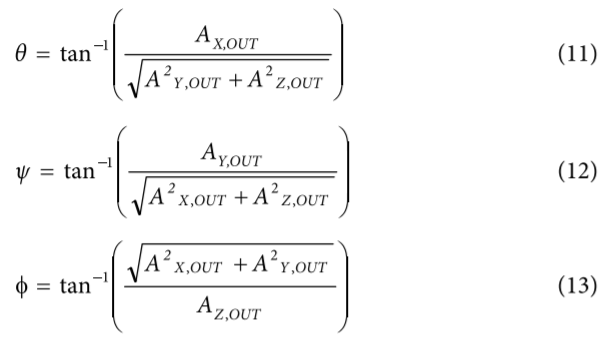
等式13中操作数出现明显反转，这是因为初始位置为1 g场。若需使用水平面作为z轴的参照，则可将操作数反转。角度为正表示对应的加速度计正轴指向水平面上方，而角度为负表示轴指向水平面下方。

 

由于采用反正切函数和加速度之比，因此具有双轴示例中提及的优势，也就是说有效增量灵敏度是恒定的，并且单位范围内的角度可在所有点上精确测得。

 

校准失调和灵敏度失配误差

 

本应用笔记中的分析假设采用理想加速度计。该假设等同于使用无0 g失调且具有完美灵敏度的器件——灵敏度以mV/g(模拟传感器)或LSB/g(数字传感器)表示。虽然传感器经过调节，但器件本质上是机械的，这便意味着系统完成装配后，器件上的任何静态应力都有可能影响失调和灵敏度。再加上工厂校准的限制，便有可能使误差超出应用允许的限值以外。

 

失调误差的影响

 

为了表明误差到底有多大，可以设想一下，某个双轴解决方案具有完美的灵敏度，但x轴上存在50 mg失调。0°时，x轴读数为50 mg，y轴读数则为1 g。由此计算得出的角度就是2.9°，因而会造成2.9°的误差。±180°时，x轴的读数为50 mg，y轴的读数则为−1 g。由此计算得出的角度会存在−2.9°的误差。图13所示为本例中算出的角度和实际角度之间的误差情况。失调引起的误差可能不仅大于系统所需的精度，而且还会发生变化，使简单地通过校准消除误差角变得困难。当多个轴上都存在失调时，这将会变得更为复杂。

 

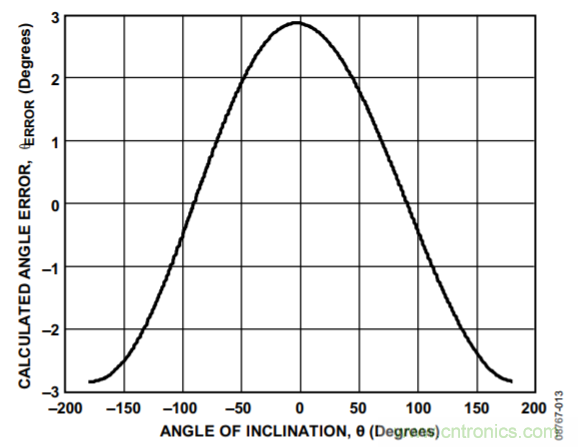
图13. 加速度计失调引起的角度计算误差

 

灵敏度失配误差的影响

 

在双轴倾斜检测应用中，由加速度计灵敏度导致的主要误差成分是目标轴之间的灵敏度差异(在单轴解决方案中，如果实际灵敏度和预期灵敏度之间存在任何偏差，则会导致出现误差)。由于使用的是x和y轴的比值，因此如果两者灵敏度相同，则可以消除大多数误差。

 

下面举例说明加速度计灵敏度失配的影响。假设某个双轴解决方案具有完美的失调调整功能，且y轴具有完美的灵敏度，但x轴的灵敏度为+5%。这表示在1 g场中，y轴读数为1 g，x轴读数则为1.05 g。图14所示为因为这种灵敏度失配而造成角度计算出现的误差情况。与失调误差类似，加速度计灵敏度失配引起的误差会在整个旋转范围内不断变化，使在计算出倾斜角后进行误差补偿变得困难。改变y轴的灵敏度会进一步增加失配，从而使误差更大。

 

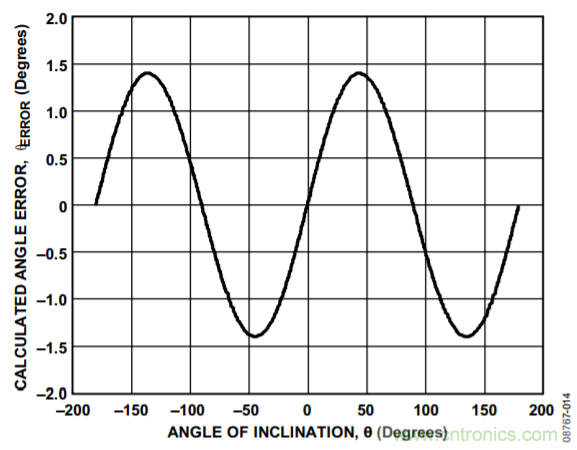
图14. 加速度计灵敏度失配引起的角度计算误差

 

基本校准技术

 

当失调引起的误差和灵敏度失配引起的误差两者相叠加时，误差可能会变得相当大，完全超出倾斜检测应用所能接受的范围。要减少这类误差，就应当对失调和灵敏度进行校准，并使用校准后的输出加速度来计算倾斜角。包括失调和灵敏度的影响后，加速度计输出变化如下：

 

 

其中：

 

AOFF表示失调误差，单位为g。

 

Gain表示加速度计的增益，理想值为1。

 

AACTUAL表示加速度计的真实加速度和目标值，单位为g。

 

一种简单的校准方法是假设增益为1并测量失调。经过此校准之后，系统的精度即会限制为未校准的灵敏度误差。这种简单的校准方法可通过将目标轴置于0 g场中并测量输出(大小等于失调)来完成。然后，应在处理信号之前从加速度计的输出中减去该值。这种方法通常称为无调头或单点校准，因为器件的典型取向会将x和y轴置于0 g场中。如果使用的是三轴器件，则应针对z轴包含至少一个调头或第二个点。

 

一种更加精确的校准方法是每个目标轴上取用两个点(三轴设计最多可取用六个点)。当某个轴处于+1 g和−1 g场中时，测得的输出如下：

 

 

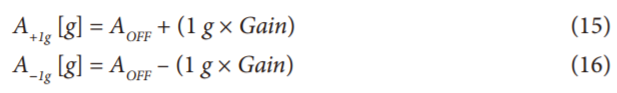
其中，失调AOFF的单位为g。

 

利用这两个点确定的失调和增益如下：

 

 

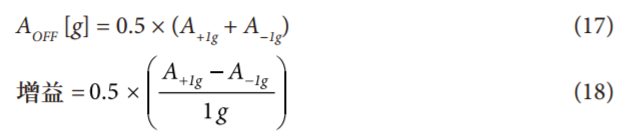
其中，+1 g和−1 g测量结果A+1g和A−1g均以g表示。

 

由于测量目标轴时，正交轴都处于0 g场，因此这种校准方法还有助于将跨轴灵敏度影响降至最低。利用这些值，首先可以从加速度计测量结果中减去失调，然后将所得结果除以增益。

 

 

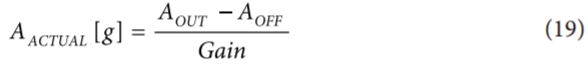
其中，AOUT和AOFF的单位为g。

 

等式15至等式19中，计算AOFF和增益时，假设加速度值A+1g和A−1g均以g表示。如果加速度单位采用mg，则等式17中AOFF的计算结果会保持不变，但等式18中增益的计算结果需要除以1000，以处理单位上的变化。

 

 

推荐阅读：